Research

Overview of Research Projects

This page is a survey of my past research projects. I favored to summarize them in simple English, making our research as accessible as possible.

Progressive Simplification of Polygonal Curves

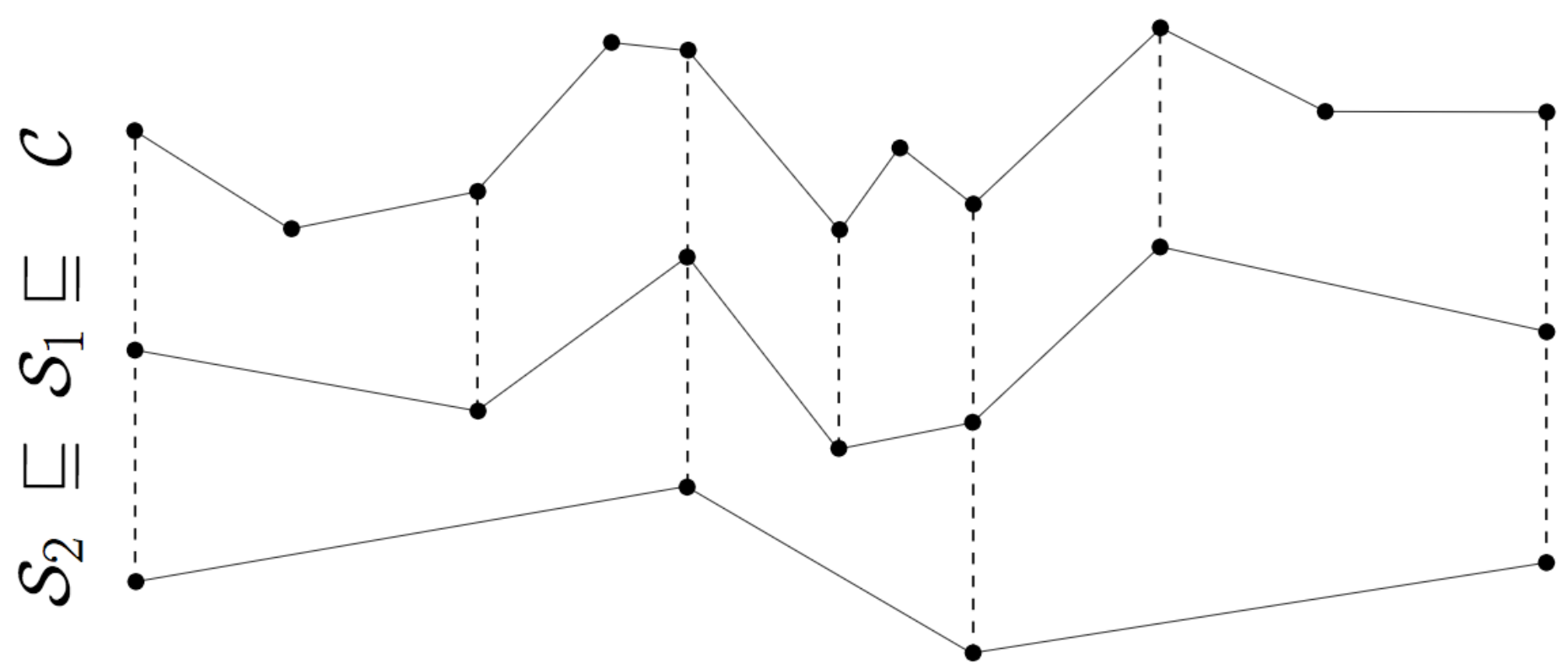
State-of-the-art map services make use of multiple zoom levels. We developed a simplification algorithm that outputs a series of simplifications across multiple spatial scales. To this end, we developed new construction techniques that boost the computations for any simplification algorithm employing shortcut graphs. We applied our algorithm to migratory trajectory of a vulture and evaluated various simplification algorithms experimentally.

References

Visual Exploration of Migration Patterns

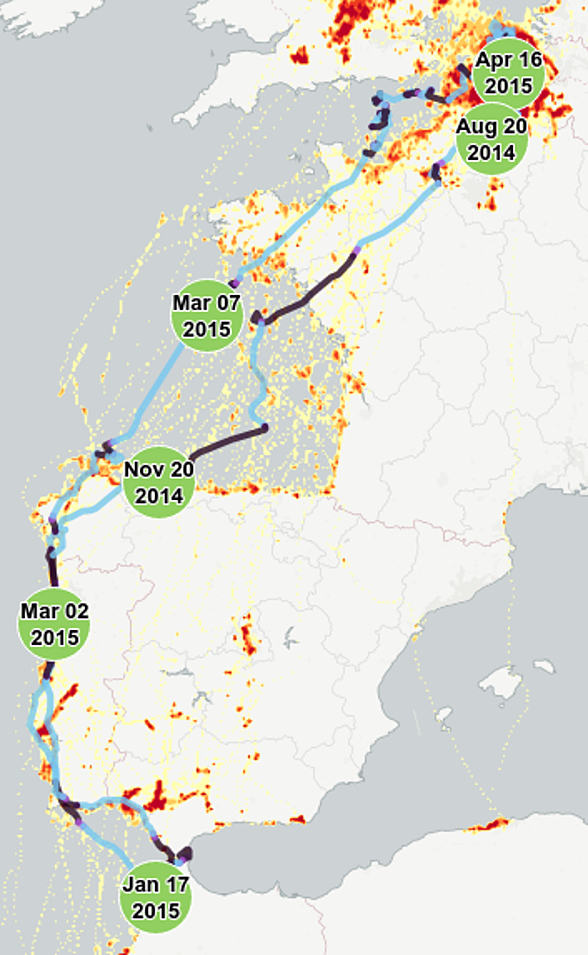
We implemented a visual analytics tool which exploits migration patterns in gull data. Migration is the spatial displacement of moving objects during seasons, such as winter and spring. We compute and visualize a trajectory aggregation (1), a density map (2) on top of geographical maps, a calendar view (3) and a list of gulls (4). Our evaluation with an expert user in ecology shows that our approach helps ecologists in identify interesting moving objects.

References

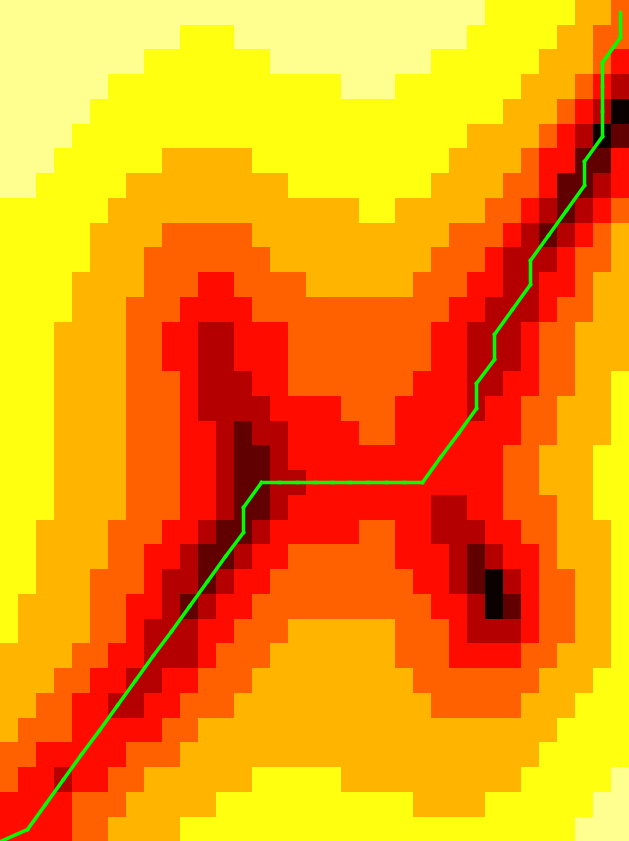
Lower Bounds on Fréchet Distance and Simplification

We have proven lower bounds for two curve problems. A lower bound of a computational problem help researchers in theory and practice to understand limits of exact computations and to get insights whether approximation algorithms can be designed easily. We showed that we cannot compute an optimal simplification in subquadratic time and that we cannot compute the Fréchet distance for k curves in less than O(n^k) time. We assume for both results that the Strong Exponential Time Hypothesis (SETH) holds.

References

Visual Analytics of Delays and Interaction

We developed a visual analytics approach to analyze and visualize interaction events between two (and three) trajectories. Interaction is the interdependence between two moving objects. We were interested in action-reaction patterns where one trajectory is reacting after a delay in time. We applied and evaluated our approach on pigeon data ultimate frisbee data.

References

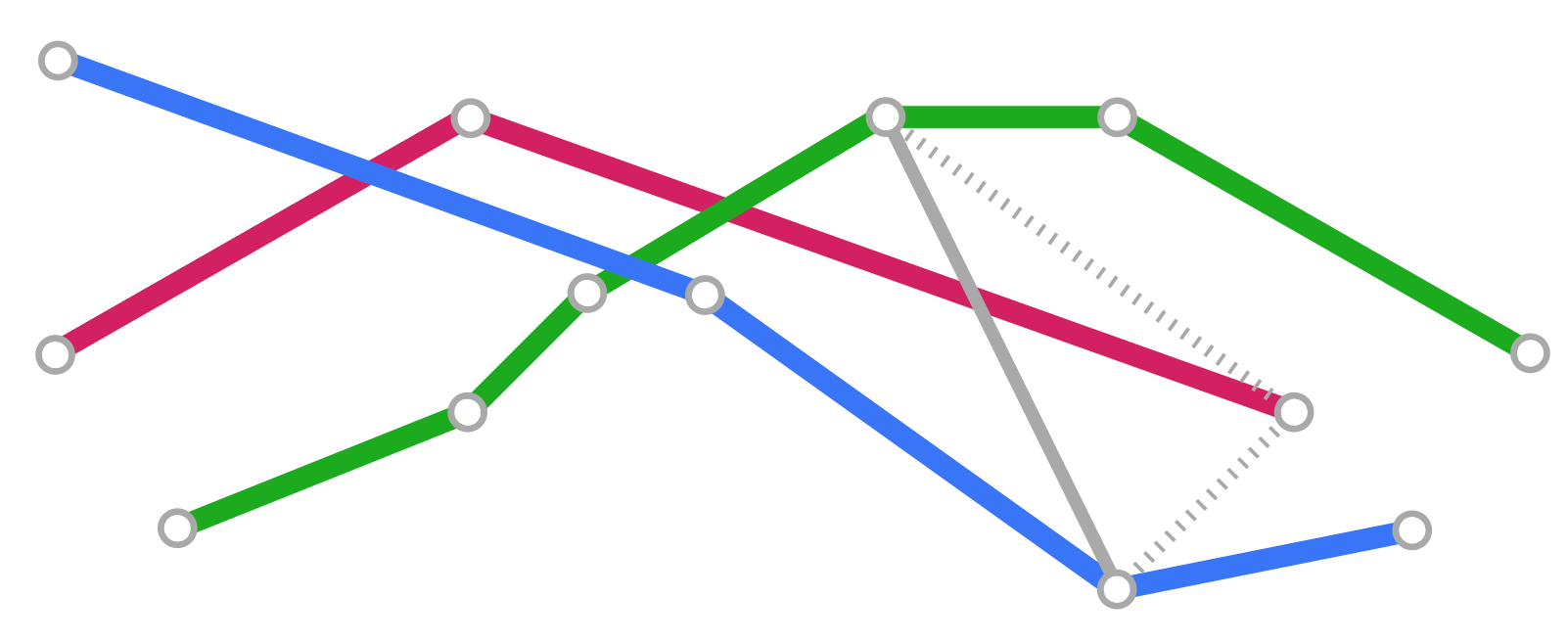
Low-Crossing Spanning Trees

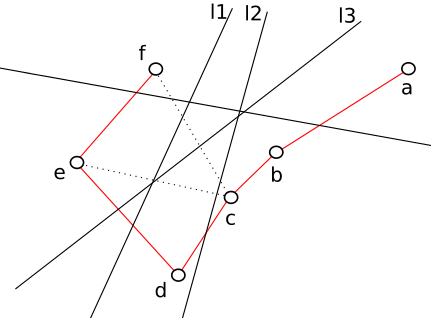We studied the problem of computing a spanning tree that minimizes crossings with lines in the plane. The problem of finding a spanning tree with minimal crossing number is NP-hard. We conducted an experimental evaluation of various algorithms and approximations in form of linear programs.